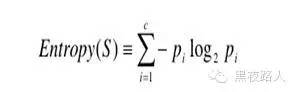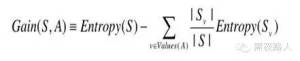From: http://blog.csdn.net/heiyeshuwu/article/details/46991273
[原]【原创】机器学习算法之:决策树
Posted: July 21st, 2015, 8:12pm CEST
机器学习算法之:决策树
作者:jmz (360电商技术)
1 概览
决策树学习是一种逼近离散值目标函数的方法,在这种方法中学习到的函数被表示为一棵决策树:
1) 学习析取表达式,能再被表示为多个if-then的规则,以提高可读性。
2) 对噪声数据有很好的适应性。–统计特性
3) 决策树学习方法搜索完整表示的假设空间(一个有效的观点是机器学习问题经常归结于搜索问题,即对非常大的假设空间进行搜索、已确定最佳拟合到观察到的数据),从而避免了受限假设空间的不足。决策树学习的归纳偏置(有兴趣参考“归纳偏置”,“奥坎姆剃刀问题”相关问题更详细的描述)是优先选择较小的树。
2 决策树表示
决策树通过把实例从根结点排列(如何选择排列次序是决策树算法的核心)到某个叶子结点来分类实例,叶子结点即为实例所属的分类。树上的每一个结点指定了对实例的某个属性的测试,并且该结点的每一个后继分支对应于该属性的一个可能值。
如,一颗根据天气情况判断是否参加打网球的决策树如下:
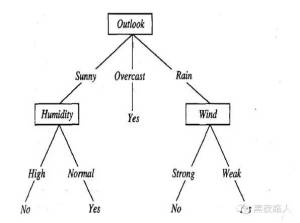
例如,下面的实例:将被沿着这棵决策树的最左分支向下排列,因而被评定为反例(也就是这棵树预测PlayTennis=No) 。
通常决策树代表实例属性值约束的合取(conjunction)的析取式(disjunction)。从树根到树叶的每一条路径对应一组属性测试的合取,树本身对应这些合取的析取,该决策树对应于以下表达式:
(Outlook=Sunny ٨Humidity=Normal)
٧(Outlook=Overcast)
٧(Outlook=Rain٨ Wind=Weak)
3 适用场景
不同的决策树学习算法可能有这样或那样的不太一致的能力和要求,但根据以上分析描述不难看出、决策树学习最适合具有以下特征的问题:
1) 实例是由“属性-值”对(pair)表示的。最简单的决策树学习中,每一个属性取少数的分离的值(例如,Hot、Mild、Cold)。
2) 目标函数具有离散的输出值。
3) 可能需要析取的描述,如上面指出的,决策树很自然地代表了析取表达式。
4) 训练数据可以包含错误。决策树学习对错误有很好的适应性,无论是训练样例所属的分类错误还是描述这些样例的属性值错误。
5) 训练数据可以包含缺少属性值的实例。
已经发现很多实际的问题符合这些特征,所以决策树学习已经被应用到很多问题中。例如根据疾病分类患者;根据起因分类设备故障;根据拖欠支付的可能性分类贷款申请。对于这些问题,核心任务都是要把样例分类到各可能的离散值对应的类别中,因此经常被称为分类问题
4 基本的决策树学习算法
大多数决策树学习算法是一种核心算法的变体、该算法采用自顶向下的贪婪搜索遍历可能的决策树空间。决策树构造过程是从“哪一个属性将在树的根结点被测试?”这个问题开始的。
1) 使用统计测试来确定每分类能力最好的属性被选作树的根结点的测试。
2) 为根结点属性的每个可能值产生一个分支,并把训练样例排列到适当的分支(也就是,样例的该属性值对应的分支)之下。
3) 重复整个过程,用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。
这形成了对决策树的贪婪搜索,也就是算法从不回溯重新考虑以前的选择。下图描述了该算法的一个简化版本:

1. 哪个属性是最佳的分类属性?
ID3 算法的核心问题是选取在树的每个结点要测试的属性,我们希望选择的是最有助于分类实例的属性。
1) 用熵度量样例的纯度
为了精确地定义信息增益,我们先定义信息论中广泛使用的一个度量标准,称为熵(entropy),它刻画了任意样例集的纯度(purity)。给定包含关于某个目标概念的正反样例的样例集S,那么S 相对这个布尔型分类的熵为:
Entropy(S) = -p⊕log2p⊕ -pΘlog2pΘ
其中p⊕是在S 中正例的比例,pΘ是在S 中负例的比例。在有关熵的所有计算中我们定义0log0 为0。
举例说明,假设S 是一个关于某布尔概念的有14 个样例的集合,它包括9 个正例和5 个反例(我们采用记号[9+,5-]来概括这样的数据样例)。那么S 相对于这个布尔分类的熵(Entropy)为:
Entropy ([9+, 5−]) = −(9 / 14) log 2 (9 /14) − (5 / 14) log 2(5 / 14) =0.940
注意,如果S 的所有成员属于同一类,那么S 的熵为0。例如,如果所有的成员是正的 ( p⊕=1 ) , 那么 pΘ 就是 0 , 于是 Entropy(S) =− 1 ⋅ log ( 1 ) − (0) ⋅log (0) = −1 ⋅ 0 − 0 ⋅ log 0 = 0 。
另外,当集合中正反样例的数量相等时熵为1。如果集合中正反例的数量不等时,熵介于0 和1 之间。下图显示了关于某布尔分类的熵函数随着p⊕从0 到1 变化的曲线。
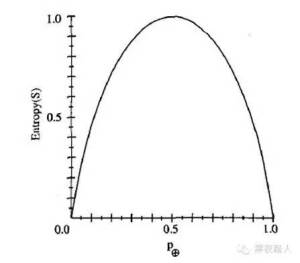
信息论中熵的一种解释是,熵确定了要编码集合S 中任意成员(即以均匀的概率随机抽出的一个成员)的分类所需要的最少二进制位数。举例来说,如果p ⊕ 是1,接收者知道抽出的样例必为正,所以不必发任何消息,此时的熵为0。另一方面,如果是p⊕0.5,必须用一个二进制位来说明抽出的样例是正还是负。如果p⊕ 是0.8,那么对所需的消息编码方法是赋给正例集合较短的编码,可能性较小的反例集合较长的编码,平均每条消息的编码少于1 个二进制位。
更一般的,如果目标属性具有c个不同的值,那么S 相对于c 个状态(c-wise)的分类的熵定义为:
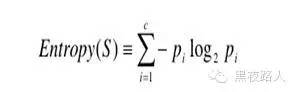
2) 用信息增益度量期望的熵降低
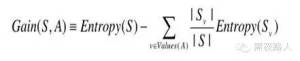
已经有了熵作为衡量训练样例集合纯度的标准,现在可以定义属性分类训练数据的效力的度量标准。这个标准被称为“信息增益”。简单的说,一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低。
其中Values(A)是属性A 所有可能值的集合。
Sv是S 中属性A 的值为v 的子集(也就是,S v ={s∈S|A(s)=v})。
请注意,等式的第一项就是原来集合S 的熵,第二项是用A 分类S 后熵的期望值。这个第二项描述的期望熵就是每个子集的熵的加权和。|Sv |权值为属于Sv 的样例占原始样例S 的比例。所以Gain(S,A)是由于知道属性A的|S |值而导致的期望熵减少。
换句话来讲,Gain(S,A)是由于给定属性A 的值而得到的关于目标函数值的信息。当对S 的一个任意成员的目标值编码时,Gain(S,A)的值是在知道属性A 的值后可以节省的二进制位数。
信息增益正是ID3 算法增长树的每一步中选取最佳属性的度量标准。下图概述了如何使用信息增益来评估属性的分类能力。在这个图中,计算了两个不同属性:湿度(Humidity)和风力(Wind)的信息增益:

2. 算法示例
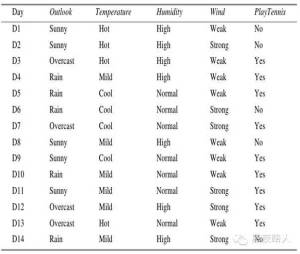
为了演示ID3 算法的具体操作,训练样例入下图。这里,目标属性PlayTennis 对于不同的星期六上午具有yes 和no两个值,我们将根据其他属性来预测这个目标属性值。
先考虑这个算法的第一步,创建决策树的最顶端结点。哪一个属性该在树上第一个被测试呢?ID3算法计算每一个候选属性(也就是Outlook,Temperature,Humidity,和Wind)的信息增益,然后选择信息增益最高的一个。所有四个属性的信息增益为:
Gain(S,Outlook)=0.246
Gain(S,Humidity)=0.151
Gain(S,Wind)=0.048
Gain(S,Temperature)=0.029
其中S 表示来自下图的训练样例的集合。
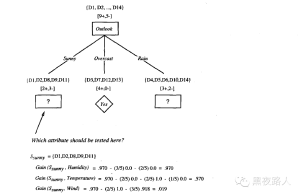
根据信息增益标准,属性Outlook 在训练样例上提供了对目标属性PlayTennis 的最好预测。所以,Outlook 被选作根结点的决策属性,并为它的每一个可能值(也就是Sunny,Overcast 和Rain)在根结点下创建分支。
同时画出的还有被排列到每个新的后继结点的训练样例。注意到每一个Outlook=Overcast 的样例也都是PlayTennis 的正例。所以,树的这个结点成为一个叶子结点,它对目标属性的分类是PlayTennis=Yes。相反,对应Outlook=Sunny 和Outlook=Rain 的后继结点还有非0的熵,所以决策树会在这些结点下进一步展开。
对于非终端的后继结点,再重复前面的过程选择一个新的属性来分割训练样例,这一次仅使用与这个结点关联的训练样例。已经被收编入树的较高结点的属性被排除在外,以便任何给定的属性在树的任意路径上最多仅出现一次。对于每一个新的叶子结点继续这个过程,直到满足以下两个条件中的任一个:
1) 所有的属性已经被这条路径包括
2) 与这个结点关联的所有训练样例都具有同样的目标属性值(也就是它们的熵为0)
下图演示了算法的求解过程:
5 用搜索的观点看决策树学习
与其他的归纳学习算法一样,ID3算法可以被描述为从一个假设空间中搜索一个拟合训练样例的假设。被ID3 算法搜索的假设空间就是可能的决策树的集合。ID3算法以一种从简单到复杂的爬山算法遍历这个假设空间。从空的树开始,然后逐步考虑更加复杂的假设,目的是搜索到一个正确分类训练数据的决策树。引导这种爬山搜索的评估函数是信息增益度量。下图描述了这种搜索:
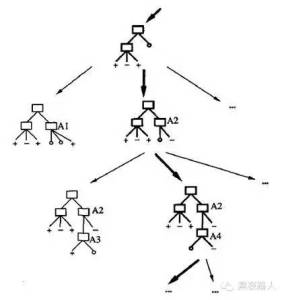
可以通过ID3算法的搜索空间和搜索策略深入认识这个算法的优势和不足。
1) ID3算法中的假设空间包含所有的决策树, 避免了搜索不完整假设空间(说明一下:有些算法是搜索不完整假设空间的、具体参考<<机器学习>>这本书)的一个主要风险:假设空间可能不包含目标函数。
2) 当遍历决策树空间时,ID3仅维护单一的当前假设。因为仅考虑单一的假设,ID3算法失去了表示所有一致假设所带来的优势。(说明一下:意思就是说它不能判断有没有其他的决策树也是与现有的训练数据一致的,或者使用新的实例查询来最优地区分这些竞争假设)
3) 在搜索中不进行回溯。每当在树的某一层次选择了一个属性进行测试,它不会再回溯重新考虑这个选择。所以,它易受无回溯的爬山搜索中常见风险影响:收敛到局部最优的答案,但不是全局最优的。
4) 搜索的每一步都使用当前的所有训练样例,以统计为基础决定怎样精化当前的假设。这与那些基于单独的训练样例递增作出决定的方法不同。使用所有样例的统计属性(例如,信息增益)的一个优点是大大减小了对个别训练样例错误的敏感性。
6 决策树学习的归纳偏置(参见归纳偏置相关论述)
1从观测到的训练数据泛化以分类未见实例的策略是什么呢?
换句话说,它的归纳偏置是什么?
如果给定一个训练样例的集合,那么通常有很多决策树与这些样例一致。所以,要描述ID3 算法的归纳偏置,应找到它从所有一致的假设中选择一个的根据。ID3从这些决策树中选择哪一个呢?它选择在使用简单到复杂的爬山算法遍历可能的树空间时遇到的第一个可接受的树。
概略地讲,ID3的搜索策略为
a) 优先选择较短的树而不是较长的
b) 选择那些信息增益高的属性离根结点较近的树。
在ID3 中使用的选择属性的启发式规则和它遇到的特定训练样例之间存在着微妙的相互作用,由于这一点。很难准确地刻划出ID3 的归纳偏置。然而我们可以近似地把它的归纳偏置描述为一种对短的决策树的偏好。
近似的ID3 算法归纳偏置:较短的树比较长的优先
事实上,我们可以想象一个类似于ID3的算法,它精确地具有这种归纳偏置。考虑一种算法,它从一个空的树开始广度优先搜索逐渐复杂的树,先考虑所有深度为1 的树,然后所有深度为2的,……。一旦它找到了一个与训练数据一致的决策树,它返回搜索深度的最小的一致树(例如,具有最少结点的树)。让我们称这种广度优先搜索算法为BFS-ID3。BFS-ID3寻找最短的决策树,因此精确地具有“较短的树比较长的得到优先”的偏置。ID3可被看作BFS-ID3的一个有效近似,它使用一种贪婪的启发式搜索企图发现最短的树,而不用进行完整的广度优先搜索来遍历假设空间。
因为ID3 使用信息增益启发式规则和“爬山”策略,它包含比BFS-ID3更复杂的偏置。尤其是,它并非总是找最短的一致树,而是倾向于那些信息增益高的属性更靠近根结点的树。ID3 归纳偏置的更贴切近似:
较短的树比较长的得到优先。那些信息增益高的属性更靠近根结点的树得到优先。
2. 为什么优先短的假设?
奥坎姆剃刀:优先选择拟合数据的最简单假设。
为什么应该优先选择较简单的假设呢?科学家们有时似乎也遵循这个归纳偏置。例如物理学家优先选择行星运动简单的解释,而不用复杂的解释。对这个问题并没有一个确定性的定论和证明、有兴趣的可以参考相关资料。
7 决策树常见问题
1. 避免过度拟合数据
对于一个假设,当存在其他的假设对训练样例的拟合比它差,但事实上在实例的整个分布(也就是包含训练集合以外的实例)上表现的却更好时,我们说这个假设过度拟合训练样例。
这种情况发生的一种可能原因是训练样例含有随机错误或噪声。事实上,当训练数据没有噪声时,过度拟合也有可能发生,这种情况下,很可能出现巧合的规律性。
有几种途径用来避免决策树学习中的过度拟合。它们可被分为两类:
a) 及早停止增长树法,在ID3 算法完美分类训练数据之前停止增长树;
b) 后修剪法,即允许树过度拟合数据,然后对这个树后修剪。
一个常见的做法是错误率降低修剪:考虑将树上的每一个结点作为修剪的候选对象。修剪一个结点由以下步骤组成:删除以此结点为根的子树;使它成为叶子结点;把和该结点关联的训练样例的最常见分类赋给它。仅当修剪后的树对于验证集合的性能不差于原来的树时才删除该结点。这样便使因为训练集合的巧合规律性而加入的结点很可能被删除,因为同样的巧合不大会发生在验证集合中。反复地修剪结点,每次总是选取它的删除可以最大提高决策树在验证集合上的精度的结点。继续修剪结点直到进一步的修剪是有害的。
2. 合并连续值属性
把连续值属性的值域分割为离散的区间集合。其实本质还是处理离散值、只是将连续值划分为离散值。
3. 属性选择的其他度量标准
信息增益度量存在一个内在偏置,它偏袒具有较多值的属性。举一个极端的例子,考虑属性Date,它有大量的可能值(例如March 4,1979)。要是我们把这个属性加到数据中,它会在所有属性中有最大的信息增益。
这是因为单独Date就可以完全预测训练数据的目标属性。于是这个属性会被选作树的根结点的决策属性并形成一棵深度为一级但却非常宽的树,这棵树可以理想地分类训练数据。当然,这个决策树对于后来数据的性能会相当差,因为尽管它完美地分割了训练数据,但它不是一个好的预测器(predicator)。
属性Date出了什么问题了呢?简单地讲,是因为它太多的可能值必然把训练样例分割成非常小的空间。因此,相对训练样例,它会有非常高的信息增益,尽管对于未见实例它是一个非常差的目标函数预测器。避免这个不足的一种方法是用其他度量,而不是信息增益,来选择决策属性。关于选取其他度量属性度量标准、参见参考资料。
4. 处理缺少属性值的训练样例
在某些情况下,可供使用的数据可能缺少某些属性的值。例如,在医学领域我们希望根据多项化验指标预测患者的结果,然而可能仅有部分患者具有验血结果。在这种情况下,经常需要根据此属性值已知的其他实例,来估计这个缺少的属性值。
处理缺少属性值的一种策略是赋给它结点n 的训练样例中该属性的最常见值。另一种策略是可以赋给它结点n 的被分类为c(x)的训练样例中该属性的最常见值。
5. 处理代价不同的属性
在某些学习任务中,实例的属性可能与代价相关。例如,在学习分类疾病时我们可能以这些属性来描述患者:体温、活组织切片检查、脉搏、血液化验结果等。这些属性在代价方面差别非常大,不论是所需的费用还是患者要承受的不适。对于这样的任务,我们将优先选择尽可能使用低代价属性的决策树,仅当需要产生可靠的分类时才依赖高代价属性。考虑代价的相关算法参见参考资料。
参考资料:
1<<机器学习>> Tom M. Mitchell
2<> Andrew Ng
课程翻译:
http://v.163.com/special/opencourse/machinelearning.html
讲义下载:
http://openclassroom.stanford.edu/MainFolder/CoursePage.php?course=MachineLearning
<完>
————————————————————————————-
黑夜路人,一个关注开源技术、乐于学习、喜欢分享的程序员
博客�� [blog.csdn.net]
微博�� [weibo.com]
微信:heiyeluren2012
想获取更多IT开源技术相关信息,欢迎关注微信!
微信二维码扫描快速关注本号码:
作者:heiyeshuwu 发表于2015/7/21 20:12:43 原文链接 阅读:35 评论:0 查看评论